Bayes theorem (3)

Fast Bayes
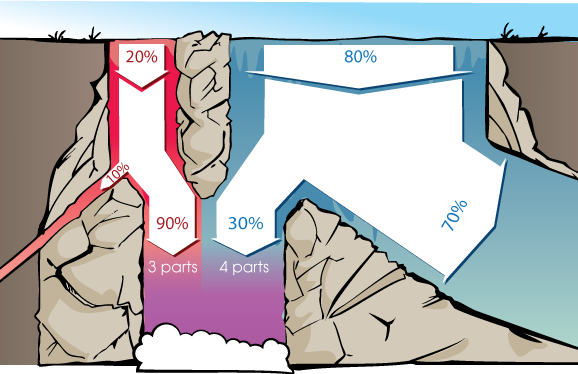
The above image shows the same Diseasitis problem in the form of a picture. Initially we have from a population, 20% who have diseasitis, and 80% not. 90% of the people with Diseasitis turn the tongue-depressor black. 30% of the people without Diseasitis turn the tongue depressor black.
We start with 4 times as much as blue water, than red water.
$ Red:blue :: 1:4
90% of the red water collects into the common pool and 30% of the blue water collects into the common pool (people who turn the tongue depressor black). Each molecule of red water is 90% likely to make it to the pool. Each molecule of blue water is 30% likely to make it to the pool. In essence we see that red water molecule is 3 times as likely as blue water molecule (90%/30%). This we term as relative likelihood. When this is multiplied by the prior propotions we get the final proportions of the water in the common pool.
$ Relative likelihood * prior proportions = (3/1)*(1/4) = 3/4
This means that for 3 parts of red water in the pool we will have 4 parts of blue water. To calculate probability of red water in the common pool to total water in the common pool we do:
$ 3/(3+4) = ~43%
As in the Diseasitis problem, out of the people who turn the tongue depressor black(which is supposed to mean that people actually have Diseasitis), only 43% will have Diseasitis. With this example it is once again clear that the tongue depressor test is extremely unreliable.