DP Claims

Lessons
-
Step one and 2
It’s good that you’re imagining concrete examples like the failing filter case. That’s step one. Now, did it serve the purpose? What purpose? The T-word. What statement were you testing?
decision making
alias paradox
But suppose, instead, that your example for decision-making was that you had to choose between a job in
with less salary but better promotion prospects than . Now, he could test the claim about "consulting experienced guys" - yeah, they could tell you roughly how much difference the extra promotion prospects would make (assuming he had a concrete example for "experienced guys", but we can assume that for our purposes). And he would reject the claim that "meditation for 20 minutes would help your decision-making" by saying that he really doesn't have even one example for it as he doesn't see how that will help him decide between extra salary and extra promotion prospects. He's not saying the claim is false; he's just saying that he hasn't seen a single example for it, let alone a ton of empirical evidence. -
Identify what the text is not saying! the text for an example to pass a claim is that it should have atleast one example!
(A job)[24b] will be (best)[24a] (for learning)[24] when you are (pushed)[25] to (improve)[26] and get (lots)[27] of (feedback from mentors)[28].
My friend currently works in Apple after he had an ivy league schooling in the US. Previously he worked in Mu Sigma a company in India, catering to the fortune 500 in the field of Data Science[24b]. He and several others who left their job in Mu Sigma 2 years later, are in some kickass positions now in the US[24a,24]. He often worked long hours and was under a lot of pressure to deliver[25,26] for the fortune 500 companies. Even on holiday trips he had his laptop to do meetings to make changes or inform his findings[27,28].
squeezed lots of feedback together? Should have I done it separately? can you show me how?
Get a concrete example and test the claim:
(A job will be best for learning)[1] when (you are pushed to improve)[2] and (get lots of feedback from mentors)[3].
The claim is [1].
An example for [2] is your friend who apparently was pushed to improve. It’s not clear if the claim is that you need both [2] and [3] to get [1] or if they will independently add to [1].
An example for [3] is again your friend.
Now test the claim. You can see that, yes, he apparently did learn a lot. But is it “best for learning”? How the fuck do you test that claim? What evidence do they have for that? That would involve comparing against all other types of jobs for learning and ensuring that a job that gives [2] and [3] is “best”. That, in my opinion, is poor writing. But what do I know?
Contrast that to saying that you will learn more at such a job even if you earn less. You can think of concrete examples for that, such as friends who work for low salaries at startups but learn a fuckton about distributed systems and reproducible builds because they have to do it all by themselves. (Again, this is far from an empirical study of the entire industry, but one test > zero tests. And one test that you do right away > a hundred perfect tests that you never do.) If some guy says that startup jobs are useless because they pay much lower than big company jobs, what can you do? You can test it instantly against the concrete example you have - nope, a friend learned a lot and went on to better jobs because of his better skills even though the startup paid less.
Can you feel the difference between just reading the statement “A job will be best for learning when you are pushed to improve and get lots of feedback from mentors” and sort of agreeing with the general idea (it sounds reasonable after all) versus testing it against an actual example? Did you notice the gaping flaw in the claim “best for learning”? That is the sort of thing I claim you are likely to see only when you test against a concrete example. (An example for this claim is the episode above, where you had missed it when not testing the claim against an example and where you could see it after I pointed out a concrete test.)
-
Similar to the previous sentence about “better” we again have an issue as highlighted below.
(This)[1] (has led)[2] to some engaged users to (focus on options like consulting)[3], (software engineering)[4], and (tech entrepreneurship)[5], when actually we think (these are rarely the best early career options if you’re focused on our top problems areas)[6].
The claim is [2] (along with [3], [4], [5], and [6]). You have to test that the claim passes for at least one example for [1].
Unfortunately, [1] = wanting to gain “career capital” early in your career, which is God-knows-what. The Dutch guy who has never heard of the term “career capital”, just like 99% of the Earth’s population, just throws up his hand and says that he is simply not able to think of a concrete example for that.
Anyway, if [1] were such that you could get a concrete example for it, you would do that and check if there is at least somebody who wanted to gain “career capital” early in his career and therefore went for consulting [3], somebody who wanted that and therefore went for software engineering [4], and somebody who was like that and therefore went for tech entrepreneurship [5]. (If they don’t have a concrete example of someone who wanted to gain “career capital” early in his career and therefore went for “tech entrepreneurship”, why did they mention it?)
Next, you would test if it is indeed “rarely the best early career options if…” [6] by checking if each of the above three examples are “rarely the best early career options”. Again, that’s hard to test because you have to show some career option that is much “better” than the ones above (along which dimension? Money? Promotion prospects? #!&$*@ “Career capital”? Progress along our “top problem areas”? Hard to say, but it wasn’t I who wrote that sentence). It would be much easier to test if their claim was that it would lead to lower lifetime earnings than someone who did something else. Then, you could get the lifetime earnings for [4] and the lifetime earnings for the alternative and check if the former is lower. See how much clearer that is?
And this as well:
(This)[1] (has led)[2] to some engaged users to (focus on options like consulting)[3], (software engineering)[4], and (tech entrepreneurship)[5], when actually we think (these are rarely the best early career options if you’re focused on our top problems areas)[6].
The claim is [2] (along with [3], [4], [5], and [6]). You have to test that the claim passes for at least one example for [1].
Unfortunately, [1] = wanting to gain “career capital” early in your career, which is God-knows-what. The Dutch guy who has never heard of the term “career capital”, just like 99% of the Earth’s population, just throws up his hand and says that he is simply not able to think of a concrete example for that.
Anyway, if [1] were such that you could get a concrete example for it, you would do that and check if there is at least somebody who wanted to gain “career capital” early in his career and therefore went for consulting [3], somebody who wanted that and therefore went for software engineering [4], and somebody who was like that and therefore went for tech entrepreneurship [5]. (If they don’t have a concrete example of someone who wanted to gain “career capital” early in his career and therefore went for “tech entrepreneurship”, why did they mention it?)
Next, you would test if it is indeed “rarely the best early career options if…” [6] by checking if each of the above three examples are “rarely the best early career options”. Again, that’s hard to test because you have to show some career option that is much “better” than the ones above (along which dimension? Money? Promotion prospects? #!&$*@ “Career capital”? Progress along our “top problem areas”? Hard to say, but it wasn’t I who wrote that sentence). It would be much easier to test if their claim was that it would lead to lower lifetime earnings than someone who did something else. Then, you could get the lifetime earnings for [4] and the lifetime earnings for the alternative and check if the former is lower. See how much clearer that is?
-
Never let out loose statements!
It was quite taxing to come up with examples. It was very hard, this part. It took 5 phrases per hour. Very slow! Was racking my head for “examples”
Good teachers will always give a concrete example with every term they use so that students can use that to test what they learn. For example, PG doesn’t just say that a “schlep” is something tedious. He gives you a concrete example using Stripe and then tests his claim that “schlep blindness” hides many valuable startup ideas by walking through how thousands of people ignored it in favour of recipe sites and how Stripe went ahead despite all the obvious schleps involved.
After this things got way too complicated with the text so I stopped there, as it was taking too much time and I was getting no where
This section was worse than last time, but that’s good news. It means there’s a lot of room for aggressive expansion. This is exactly the kind of thing you need to focus more heavily on from now on:
I didn’t understand this part at all and couldn’t continue with giving examples, so I stop here.
I don’t understand what you mean by “I didn’t understand this part”. Given that concrete thinking means breaking a sentence into a claim and getting at least one concrete example to test that sentence, you have to specify where you failed. Were you not able to identify the claim? Were you not able to come up with one example for a particle that matched the given requirements? Lastly, were you not able to test whether the claim passed for that example? Narrow down your lack of “understanding”.
The goal seems to be not to understand principle of virtual works, but to understand what I don’t understand and where and why?
-
we can skip certain parts that are “vague” as shown below:
It (gives rise)[1] to (approximate numerical methods)[2] for the solution of both (discrete)[3] and (continuous systems)[4] in the (most natural manner)[5].
The claim is that [3] gives rise to [2] while also satisfying [5].
So, whatever concrete example you use for [3] should “give rise to” something that satisfies the test of being an “approximate numerical method”.
On top of that, the solution for [3] should do so in the “most natural manner” [5] (whatever that means; for our purposes, we can mark that as an ambiguous phrase and accept something that needs just two equations instead of six).
-
Split the “and” and “or”
You should do the same with a concrete example for [4]. Note that I split “discrete and continuous” into two phrases because they are separated by an “and”. So, you will need to test the claim [1] using one example for each.
-
Be alert at all times even when receiving praises, “it’s worth it” ;)
It took me around 5.5 hours to explain my theory of concrete thinking above and review the rest of the stuff. It’s worth it. [SST]
Mission #7
Mission #7: Your mission, should you choose to accept it, is to identify claims and get concrete examples to test them.
Primary target: The same work-related document as last time that you need to understand thoroughly but currently don’t. For each sentence, identify the claim, break up any “or” and “and” into separate phrases, get a concrete example for each, and test whether the claim is true for that concrete example.
If the author provides a running example, hold on to it for dear life and use it throughout that section or chapter. (When I said “running example”, did you think of Stripe and “schlep blindness” and did you imagine going through PG’s essay with that in mind? SS should have T-ed.)
If you don’t “understand” something, specify exactly on which part you failed.
DP Mechanical Vibrations
Source: Mechanical Vibrations by Daniel J Rixen
DP Part 1 (12)
P & E:
(The analytical approach)[1] to (mechanics)[2] is based on the (concepts of energy)[3] and (work)[4] and therefore (provides a better understanding)[5] of (mechanical phenomena)[6].
For [1], we can think of the equation of the POVW used to identify the relationship between force (F) and stiffness (k) for the truss problem below.
\[\frac{1}{2} k \times dx^2 = F\times\delta y\]
For [2]: determining the force F at equilibrium for a given stiffness
For [3]: Energy of a spring, $\frac{1}{2} k \times dx^2$
For [4]: Work done by the Force F, $F\times\delta y$
For [5]: It’s easy to see that F increases then k increases in the above equation.
Contrast this to vector mechanics, where we have to write atleast 6
equations ($\Sigma Fx=0$, $\Sigma Fy=0$ & $\Sigma M=0$ (2x)). In
these equations we also have the reaction forces at A and C involved,
and the internal forces in the truss members. We can solve all this
and get a function f(geometry, reaction force, internal force,
stiffness)=0 from which it will not be as handy to see the effect of
stiffness on the force F; as compared to f(geometry, Force, Stiffness)=0
For [6]: relation between F & k. F is directly proportional to k.
Claims
{(The analytical approach)[1] to (mechanics)[2] is based on the (concepts of energy)[3] and (work)[4]}(A)
In the example approach below[1] we see the usage of energy[3] and work[4] to identify the relationship between F and k[2].
\[\frac{1}{2} k \times dx^2 = F\times dy\]The analytical approach based on the concepts of energy and work (provides a better understanding)[5] of (mechanical phenomena)[6]}(B)
F increases, then k increases based on the analytical approach. When you contrast this to vector mechanics, you see that it is hard to see the relationship between F & k, due to the presence of reaction and internal forces.
\[\frac{1}{2} k \times dx^2 = F\times dy\]P & E:
In some sense one can say that (this)[7] (considers the system in a global sense)[8], (disregarding the specifities)[9] of the (forces)[10] associated to (kinematic constraints)[11] imposed on the (system)[12].
For [7]: the POVW equation seen above for the truss
For [8]: We look at only the input F and the output travel of spring to reach the balance the forces.
For [9]: We skip the internal forces, reaction forces at A and C for example.
For [10]: Internal forces in the truss member and the reaction forces at A & C.
For [11]: We think of the yellow plane in the above figure does not allow Point C to move in the horizontal direction
For [12]: We think of the truss members and the spring
Claims
In some sense one can say that {(this)[7] (considers the system in a global sense)[8], (disregarding the specifities)[9] of the (forces)[10] associated to (kinematic constraints)[11] imposed on the (system)[12]}(C)
The analytical approach allows for the following equation:
\[\frac{1}{2} k \times dx^2 = F\times\delta y\]which considers the system based on input work and output displacement of spring[8], not bothering about the reaction forces that are generated at C and A[9] imposed by the yellow plane[11] on the truss members[12].
DP part 2 (13)
P & E
- (It)[1] (considerably simplifies)[2] the (analytical formulation)[3] of the (motion equations)[4] for a (complex)[5a] (mechanical system)[5].
For 4, think of the motion equation of a single pendulum
$ml^2 \ddot{\theta} +mgl \sin{\theta}=0$
For 1 and 3, think of the derivation of the motion equations for a simple pendulum using the POVW approach. - pg 22 Mechanical Vibrations by Daniel Rixen
For 5, imagine a double pendulum.
For 5a: With a simple pendulum we deal with a 1x1 matrix (basically not a matrix) in the derivation, which is very easy to work out by hand. But with a double pendulum, we deal with 2x2 matrices which are hard to keep track of, in the derivation of motion equations.
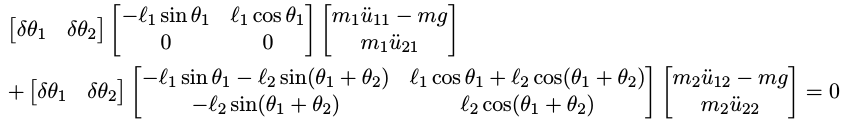
For 2: When we use the POVW to derive the motion equations of a double pendulum we have 2 equations in the end which need to be solved. When we use the newton-euler equations we quickly see that we need to construct 6 equations and need to solve them simultaneously.
Claims
Analytical approach simplifies the analytical formulation of motion equations for complex systems
When we use the POVW to derive the motion equations of a double pendulum we have 2 equations in the end which need to be solved. When we use the newton-euler equations we quickly see that we need to construct 6 equations and need to solve them simultaneously.
P & E
- (It)[6a] (gives rise to)[6] (approximate)[7a] (numerical methods)[7] for the (solution)[8] of both (discrete)[9] and (continuous systems)[10] in the (most natural manner)[11], as will be later explained in Chapters 5 and 6.
For 6a, we think of the derivation of motion equations for a double pendulum using the POVW.
for 6, we imagine giving the output of the analytical approach (the differential equations) to MATLAB to solve (because it takes too much effort to solve by hand)
For 7a,
“Numerical solution:
let’s guess 𝑥=1: 𝑓(1)=1−5=−4. A negative number. Let’s guess 𝑥=6: 𝑓(6)=6−5=1. A positive number.
The answer must be between them. Let’s try 𝑥=6+12: 𝑓(72)<0 So it must be between 72 and 6…etc.
This is called bisection method.” - Stack’
Here I should actually try to show solving the equation of motion using exact and numerical methods and show what is meant by approximation, but I need a few hours to recollect how to use them, so I have not done them
For 7, Runge Kutta method
For 8: Solution for $ml^2 \ddot{\theta} + mgl \sin{\theta}=0$ will look
something like $\theta(t)=\theta_0 \cos{(\omega t + \phi)}$, where
$\omega$ and $\phi$ need to be determined.
For 9, we think of a double pendulum
For 10, we think of a beam with a time-varying force $F=F_0
\sin{\omega t}$
For 11, it is not clear what the intention of the author is, so we skip it
I don’t know what example to give for “gives rise to”! Does it need an example? I am here thinking what does “giving rise to look like”
Claim A
- (It)[6a] (gives rise to)[6] (approximate)[7a] (numerical methods)[7] for the (solution)[8] of both (discrete)[9] and (continuous systems)[10] in the (most natural manner)[11], as will be later explained in Chapters 5 and 6.
Claim AA: Analytical approach gives rise to approximate numerical methods for the solution of discrete systems.
Claim AB: Analytical approach gives rise to approximate numerical methods for the solution of continuous systems.
If you take a double pendulum[9], and produce the motion equations with POVW[6a], you get
When you give this to a MATLAB[6] it will use Runge-Kutta (or similar techniques)[7,7a] to find the $\theta_1$ & $\theta_2$ at say t=1s [8].
A continuous system like a beam with a varying load is split into finite discrete elements (100 bar elements), following which it is treated like a discrete system which gives rise to “approximate NM” as above.
DP Part 3 (32)
P&E
Let us consider a (particle of mass m)[1], (submitted to a force field X)[2] of (components Xi)[3]. The (dynamic)[4a] (equilibrium)[4] of the (particle)[1] can be expressed in (d’Alembert’s form)[5]:
$m \ddot{u_1} - X_i $, where ui represents the (displacement of the particle)[6].
For 1, we imagine a simple pendulum
For 2, we imagine the pendulum being subjected to gravity alone, i.e., a force $mg$ in the downward direction
For 3, the force field can be denoted as [0,mg]
For 4a, when the pendulum is being pulled to a height h and let go, it keeps moving
For 4, we imagine the pendulum being pulled to a height h and let go
of. There is a force $mg \sin{\theta}$ on the ball countered by an equal
opposite force. Hence equilibrium.
For 5, the dynamic equilibrium in the Y is written as $T
\cos{\theta} - mg - m\ddot{u_1} = 0$ and in the X direction written
mas $ T \sin{\theta} - m \ddot{u_2} = 0 $
For 6, we imagine the pendulum moving from the mean position to a position $\theta=90^\circ$. The displacement, $u_i=L$ as it is measured from the mean position
The claim: dynamic equilibrium of a particle can be expressed in d’Alembert’s form
The example proving the claim: A pendulum subjected to gravity being written in the d’Alhembert’s form.
the dynamic equilibrium in the Y is written as $T
\cos{\theta} - mg - m\ddot{u_1} = 0$ and in the X direction written
as $ T \sin{\theta} - m \ddot{u_2} = 0 $
P&E
Let us next imagine that the (particle)[1] follows during the time interval [t1 , t2 ] a (motion trajectory)[2] $ui^*(t)$ (distinct from the real one ui(t))[3]. (This)[4a] (allows us to define)[4b] the (virtual displacement)[4] of the (particle)[5] by the (relationship: $\delta u_i(t) = u_i^*(t) – u_i(t)$)[6]
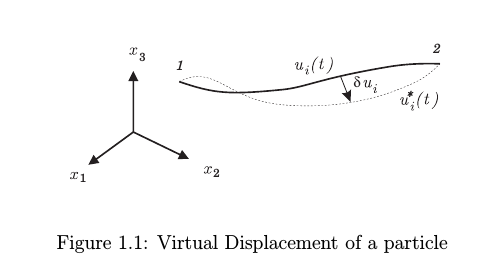
For 1 & 5: we imagine a simple pendulum
For 2, We imagine the pendulum like below making an S shape between two points A and B on the spherical surface
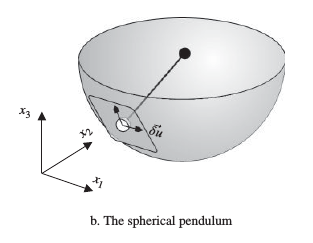
For 3, we imagine the same pendulum making a C shape between the same A and B
For 4a, we think of the 2 distinct trajectories [2] and [3].
For 4: I hear people say it is an “infinitesimal” displacement. I see it as something that houses the direction information (tangents) as shown above. And then I go to the equations straight.
The VD can also be split into X and Y components, displacement in the X direction is given by $u_2=L \sin{\theta}$, the virtual displacement is given by differentiating as $\delta u_2=L \cos{\theta}$.
This is just an equation, I don’t have an example for what it is supposed to look like, when I think of a pendulum, I don’t understand what it means to subtract two paths and say that this is the virtual displacement
For 6, I don’t know how to get $\delta u_2=L \cos{\theta}$, from [2] and [3] as shown in figure 1.1 above. How when you subtract 2 trajectories you get the virtual displacement.
So, there seem to be 2 claims:
[2] and[3] allows to define the (virtual displacement)[4]
I don’t know how [2] and [3] allow for the definition of [4]. How subtracting any 2 random trajectories is supposed to give the virtual displacement.
[4] can be obtained from [6]
I have not one example for this. It is the same as previous claim.
I spent >2 hrs on this particular part and was not able to produce examples for [6] and [4a]. It was weird that the youtube and stackexhange I referred, were wanting to talk only in pure abstract terms without providing one single running example
</br>
P&E
(By its very definition)[7], (the virtual displacement $δu_i$)[7a] is (arbitrary for t1 < t < t2)[8]. However, let us suppose that the (varied trajectory)[9] and the real one both( pass through the same points at the ends of the time interval)[10]. The(end conditions)[11] then take the (form)[12]: $\delta u_i(t_1)=\delta u_i(t_2)=0$
For 7, No idea
For 7a, we imagine the same virtual displacement as before for a simple pendulum.
For 8, I can’t think of what it means in the context of a simple pendulum, as there are only 2 paths as explained in 9.
For 9, we imagine the pendulum going counterclockwise from the mean position to $\theta=90^\circ$
For 10, we imagine the pendulum going from mean position to say $\theta=90^\circ$ but in the clockwise direction.
For 11, the difference in trajectories at $\theta=0^\circ$ & $\theta=30^\circ$ are equal to 0.
For 12, we already have “$\delta u_i(t_1)=\delta u_i(t_2)=0$”
Claims
(By its very definition)[7], (the virtual displacement $δu_i$)[7a] is (arbitrary for t1 < t < t2)[8]
No examples!
The(end conditions)[11] take the (form)[12]: $\delta u_i(t_1)=\delta u_i(t_2)=0$, if the real and virtual trajectory cross the same point at t_1 and t_2.
When paths [9] and [10] are subtracted only at the ends, they will give [12] for the case of pendulum.
P&E
Let us next (multiply)[1a] the (dynamic equilibrium equations)[1] by the associated (virtual displacement)[2] and (sum over the components)[3]. The (virtual work)[4b] (expression)[4] results: $\sum_{i=1}^{3} (m \ddot{u_i} - X_i) \delta u_i=0 $, i.e., (The virtual work)[5] produced by the (forces)[6] acting on the (particle)[7] during a (virtual displacement δui)[8] is (equal to zero)[9].
For 1, we imagine the pendulum and the dynamic equilibrium equations
written in Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$ and in the
X direction written as $ T \sin{\theta} - m \ddot{u_2} = 0$
For 2 & 8, we imagine the following virtual displacements for a simple pendulum.

For 1a, 3 and 4: $(T \cos{\theta} - mg - m \ddot{u_1}) \times (-l
\sin{\theta}) + (T \sin{\theta} - m \ddot{u_2}) (l \cos{\theta}) $
For 4b,5: We imagine multiplying the forces in Y (equilibrium equation) with virtual displacements,
$(T \cos{\theta} - mg - m \ddot{u_1}) (-l \sin{\theta})$
In X,
$(T \sin{\theta} - m \ddot{u_2}) (l \cos{\theta})$
For 6,
For 7, we think of the simple pendulum.
For 9: As [1] is equal to 0, multiplying by [1] and summing continues to give 0.
The claim
(The virtual work)[5] produced by the (forces)[6] acting on the (particle)[7] during a (virtual displacement δui)[8] is (equal to zero)[9].
The claim is that if we multiply [1] by [2] and sum them for each component, we should get an expression resulting in 0 [4], which we do, as [1] is equal to 0, multiplying and summing still continues to give 0.
[4b] looks like $\sum_{i=1}^{3} (m \ddot{u_i} - X_i) \delta u_i=0$
Yes!
DP part 4 (38)
(The virtual work above)[1] represents the (scalar product)[2] between the (forces acting on the particle)[3] and the (virtual displacement δu)[4].
For 1, we imagine this:
$(T \cos{\theta} - mg - m \ddot{u_1}) \times (-l \sin{\theta}) + (T
\sin{\theta} - m \ddot{u_2}) (l \cos{\theta}) $
For 2: we imagine the multiplication and subsequent addition of two vectors in the following way. This is what is done above as well with the Forces in X and Y and the Virtual Displacements in X and Y.
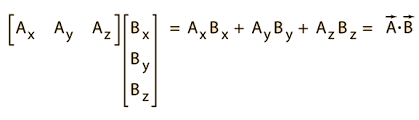
For 3, we think of the gravitational force (mg), the inertial force ($m \ddot{u}$ and the Tension for T.
For 4, we think of the same VD’s for the pendulum given by

Claims
(The virtual work above)[1] represents the (scalar product)[2] between the (forces acting on the particle)[3] and the (virtual displacement δu)[4]
The following is an example of the above claim where the Forces in X and Y are multiplied with their virtual displacements and then added.
$(T \cos{\theta} - mg - m \ddot{u_1}) \times (-l \sin{\theta}) + (T \sin{\theta} - m \ddot{u_2}) (l \cos{\theta}) $
P&E
(It)[5a] thus represents the (projection)[5] of the (equilibrium)[6] (along the direction δu)[7].
For 5a, we imagine the final virtual works equation,
$(m \ddot{u_1}-mg) (-l \sin{\theta}) + (m \ddot{u_2}) (l
\cos{\theta})=0$
For 6, we imagine the dynamic equilibrium in X and Y
Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$
X : $ T \sin{\theta} - m \ddot{u_2} = 0$
For 7:
The virtual displacement is nothing but the instantaneous direction of the pendulum at any given time. This is nothing but the direction which is perpendicular to the string.

For 5, When you “project” a vertical line on to a horizontal plane you get 0
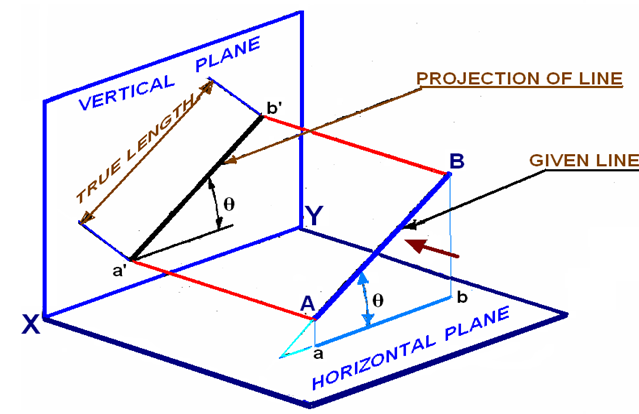
Similarly when you project the Tension onto the virtual displacement (which is $\perp$’r to the Tension, then you get 0 as seen in the following:
Equation M: $(T \cos{\theta} - mg - m \ddot{u_1}) \times (-l \sin{\theta}) + (T
\sin{\theta} - m \ddot{u_2}) (l \cos{\theta}) $
The tension terms cancel out and it becomes: $(m \ddot{u_1}-mg) (-l
\sin{\theta}) + (m \ddot{u_2}) (l \cos{\theta})=0$
Claim
(It)[5a] thus represents the (projection)[5] of the (equilibrium)[6] (along the direction δu)[7].
As seen with the above equations, the projection of equilibrium along the virtual displacement kills Tension as it is perpendicular to the virtual displacement at all angles. Hence 5a, represents a PROJECTION.
P&E
If the (virtual work equation)[8] is (satisfied)[13] for (all variations δui)[9], then the (trajectory ui(t))[10] (satisfies)[14] the (dynamic equilibrium)[11] (in all directions)[12].
For 8 we think of,
$(m \ddot{u_1}-mg) (-l \sin{\theta}) + (m \ddot{u_2}) (l
\cos{\theta})=0$
For 9, I don’t know what it means in the case of a simple pendulum
For 10, we think of moving from $\theta=0^\circ$ to $\theta=30^\circ$
For 11, we imagine the dynamic equilibrium in X and Y
Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$
X : $ T \sin{\theta} - m \ddot{u_2} = 0$
For 12, we think of the X and Y directions.
Don’t have examples for 13 and 14.
Claims
If the (virtual work equation)[8] is (satisfied)[13] for (all variations δui)[9], then the (trajectory ui(t))[10] (satisfies)[14] the (dynamic equilibrium)[11] (in all directions)[12].
The whole statement is the claim. Unfortunately I have no example to show.
P&E
If (no kinematical constraint)[1] is imposed onto the (particle)[3], namely if (no restriction)[4] is imposed on its (displacement)[5], the (trajectory of the material point)[6] (is determined)[7] by the (equilibrium in all directions)[8].
For 1: Imagine a ball rolling on plane, it can move beyond 100km in any directions along the plane. It has no constraints along the plane.
For 3, imagine a tennis ball.
For 4: There is no wall, or person to stop the ball
For 5, imagine the ball being hit by a bat from position 300m to 1km in the X direction. The displacement is 0.7km.
For 6, we think of the straight line the ball would move in.
For 8, If the ball is hit by a bat in the North direction (Y) and the east (X) direction with a force of 10N, the equilibrium equations are
X: $10\times\cos{45} - m_{ball}\times a_x}$
Y: $10\times\sin{45} - m_{ball}\times a_y}$
For 7, the $a_x=7m/s^2$ and $a_y=7m/s^2$ for a mass of
1kg if found from the above equations. This allows us to calculate the distance
traveled by the ball in north-east direction for, 5s as 35m [5].
Claims
Given [1], we should be able to calculate [6] from [8]
As shown above, we are able to calculate that the ball will move 35m as a result of the equilibrium equations shown in [8].
P&E
But when (kinematic constraints)[9a] are (specified)[9b] for the (particle)[9c], there exist (reaction forces)[9] (in addition)[10] to the (applied forces)[11].
For 9a, we imagine a string (of length L) on a ball[9c]. The ball cannot move $>L$ as a result of the string.
For 9b, we imagine tying the ball to the string and fixating one end of the string.
For 9, we imagine the tension force in the string
For 10, we have both Tension as well as gravity force acting on the ball
For 11, we imagine the gravitational force mg
Claims
When we have [9a], there is [9], and [11]
We look at the example of the pendulum and it checks out that it has the tension force and the gravity force. The tension force comes about due to the kinematic constraint provided by the string!
P&E
These (reaction forces)[12] are (inherent)[13] to the (constraining mechanism)[14] and (ensure)[15] that the (imposed kinematic constraints)[16] are (satisfied)[17].
For 12, we imagine the tension force.
For 13, we see that as soon as there is a string and the ball hanging, then there is a reaction force.
For 14, we imagine a string allowing the ball to move only along a circumference of circle of radius L.
For 15, The tension force is responsible for holding the ball at L by providing an equal and opposite force to gravity (in the mean position)
For 16, we write out the kinematic constraint as $r=L$
For 17, we imagine the $r=L$ and not $r<L$ and not $r>L$, i.e., the string is in tension
Claims
When there is [14] there is [12]
When there is a string and the ball is hanging, there are immediately Tension forces (reaction forces) in the string.
[12] ensures that [16] is satisfied.
The tension force[12] is responsible for holding the ball at L by providing an equal and opposite force to gravity (in the mean position), there by holding the realation $r=L$ (satisfied).
@ $r=L$, $T=mg$ for the case of the pendulum
@ $r<L$, $T=0N$ for the case of the pendulum
P&E
Those (reaction forces)[18] are (not known in advance)[19] since they (depend)[20a] on the (motion)[20] itself.
For 18, we imagine the tension in the string
For 19, the reaction forces in the below equation are unknown. They need to be computed solving for the following dynamic equilibrium equations given $\theta$ and accelerations.
Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$
X : $ T \sin{\theta} - m \ddot{u_2} = 0$
So there is a different tension force depending on whether the pendulum is rising against gravity from the mean position or falling from a height towards the mean position.
When the pendulum is just dropped from 45 degrees, the acceleration is 0 at that point, and the tension = 7 N
When the pendulum is at the mean position without any acceleration i.e, $\theta = 0^\circ$ then T=10N
For 20, \theta and \ddot{u} inform us about the motion; if theta is 0 and the acceleration is >0 then it means that the pendulum is going to move against gravity.
For 20a, $T = f(\theta $ and $ \ddot{u})$ (as in the dynamic equilibrium equations)
Claim
[18] are not known because of [20]
Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$
X : $ T \sin{\theta} - m \ddot{u_2} = 0$
In the above equation we see that $T = f(\theta$ and $ \ddot{u})$, i.e., the variables related to motion.
DP part 5 (16)
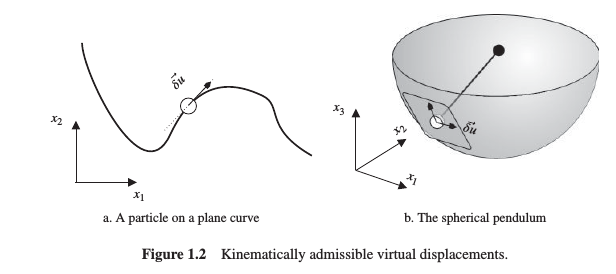
P&E
Figure 1.2 (describes)[1] a (particle)[2] (constrained)[3] to (move along a curve)[4] and a (spherical pendulum)[5] where a (particle)[6] is (constrained)[7] to have a (constant distance)[8a] with respect to a (fixed point)[8].
For 1, we think of a bowling ball moving in a gutter
For 2, we imagine a bowling ball
For 3, we imagine the gutter in the bowling alley used to guide the ball back to the main area
For 4, we imagine the gutter trajectory that goes from the main area to the bowling pins and back.
For 5, as in figure
For 6, we think of a ball
For 7, we think of the string forcing the ball to be at a radius of L at all times.
For 8a, we think of L, the distance between one end of the string to the pendulum side.
For 8, we think of the opposite end of the pendulum that is fixed.
Claims
Figure 1.2 (describes)[1] a (particle)[2] (constrained)[3] to (move along a curve)[4]
Yes!
Figure 1.2 describes (spherical pendulum)[5] where a (particle)[6] is (constrained)[7] to have a (constant distance)[8a] with respect to a (fixed point)[8].
Yes!
P&E
On one hand, the (presence)[9a] (of reaction forces)[9] (acting)[10] in the (direction of the constraint)[10a] (generally)[10c] (renders)[10b] the (equilibrium)[11] description (more complex)[12]
For 9, we imagine the Tension force in a pendulum.
For 9a, we imagine pulling on the pendulum so that there is no slack in the string, which is when the Tension in the string appears.
For 10a, for a pendulum in the mean position, we can imagine that the pendulum will not go down even if 100kN of force is applied. It will stay at L (assuming the string can handle the stress and does not deform beyond L). This downward direction is the direction of the constraint. However, if you pull in the horizontal plane, it will move, i.e., the resistance to motion is along the string.
For 10, we think about the direction of Tension force (vertical) being the same as the direction of constraint (vertical)
For 10b, I don’t know what example to give! Need help! Do I need to give an example?
For 10c, I don’t know what example to give! Need help!
For 11, we think of the same dynamic equilibrium equations for the pendulum
Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$
X : $ T \sin{\theta} - m \ddot{u_2} = 0$
For 12, due to the reaction forces, we now have an additional term to compute at every $\theta$
since those (unknown forces)[12a] must be (determined)[13] along the (entire trajectory)[14] such that (kinematical constraints)[15] are (satisfied)[16].
For 12a, we think about the Tension T,
For 13, we deal with this in the claim.
For 14, lets say you pull the pendulum to an $\theta = 30^\circ$ and let it go, it will make a to and fro trajectory
For 15, we think of the string that adds a constraint $r=L$ to the system.
For 16, explained in the claim.
Claims
On one hand, the (presence)[9a] (of reaction forces)[9] (acting)[10] in the (direction of the constraint)[10a] generally (renders)[10b] the (equilibrium)[11] description (more complex)[12] since those (unknown forces)[12a] must be (determined)[13] along the (entire trajectory)[14] such that (kinematical constraints)[15] are (satisfied)[16].
Presence of [9] along [10a] makes [11] more complex since [9] must be determined along [14] such that [15] is satisfied.
The presence of Tension forces[9] in the direction of the string[10a] adds the “T” term to the equation below. This T needs to be computed for every angle [14], making it more time consuming (more complex) than when there is no tension force.
Y : $T \cos{\theta} - mg - m \ddot{u_1} = 0$
X : $ T \sin{\theta} - m \ddot{u_2} = 0$
[12a] must be determined, such that [15] is satisfied.
@ $\theta=30^\circ$ if we want to find the Tension force, we need the
acceleration. The acceleration is in the tangential direction to the
string is $a_t = g \sin{30} = 5m/s^2$ for all angles when
$r=L$[15]. From this we calculate $\ddot{u_1} = a_t \sin{\theta} =
2.5m/s^2 $, which allows the Tension to equal to 14N.
DP 80000 hours CC (89)
Source: 80000 hours Career Guide
P&E
If you want to (increase)[1] your (social impact)[2], you face a choice: try to (make a difference right away)[4], or (invest in yourself)[5] to make a (greater impact)[6] in the (long-term)[7]. Which is (best)[8]?
For 2, we think of $$’s donated to AMF
For 1, we imagine what I am doing right now (saving 1 life per year with 4k$). Instead if I was somehow worthy of working at GiveWell I could save 24 lives per year (97k$/4k$/life) as a conservative estimate.
For 4, I imagine living in a house 300 euros cheaper than my current one, I don’t eat outside, I don’t go to India, I save as much money as I can (in my current case, that would amount to 8-10k donations).
For 5, I imagine clocking 4 hrs a day on DP for Data Science and becoming worthy of Google placement in US which possibly would earn 200k$;
For 6, we imagine donating >35% of 200k per year after 5 years which is much greater than 8k
For 7, we imagine donating this 35% until I retire from there.
For 8, we imagine donating 35% of 200k$ > 8k$
Claims
If you want [1] and [2], you face a choice, such as [4] or [5]
When we want to increase the $$ donated, we need to choose if we want to donate all we can now (8k$) or be very good in Data Science that will place you in Google for a salary of 200k.
Is the above way of writing an example of the claim, do you expect to see [1], [2], [3], [4] in the example as well?
P&E
(This)[8a] is a (complex question)[8] (and you can see more of our research here) but (we think)[9] (many)[10a] (people)[10] should focus on (investing in themselves)[11] (early in their career)[12]. Why?
For 8a, we imagine if one should go into law school, or software engineering or do charity work directly to be able to donate best
For 8, There are lawyers who work for Trump who earn >200k and there are lawyers who work for <100k, it is hard to predict which one you will be as it depends on how many cases you can win (for example)
For 9, we imagine the research explained here in 80000 hrs career guide.
For 10 & 10a, I imagine people like Peter, 22, majoring in Political Science and Psychology
For 11, I imagine people like Peter, working in programming and finance.
For 12, I imagine people like Peter who are 22 years old.
Claims
[8a] is a complex question [8]
Examples 8 and 8a inform that the claim is true.
Many people should focus on [11] early in their career (to make maximum social impact)
According to 80k hours, because Peter went into programming and Finance, he intends to donate 45k$ more than if had pursued a PhD in Political Science.
P&E
(People like to lionize)[1] the (Mozarts and Mark Zuckerbergs of the world)[2] –(people who achieved great success while young)[3] – and there are (all sorts of awards for young leaders)[4], like the Forbes 30 under 30. But (these stories)[5a] are (interesting)[5] precisely because they’re the (exception)[6]. If you want to get your (dream job)[7], then you’ll (probably)[8] need to (invest in yourself first)[9].
For 1, my cousin who is 16 says he wants to be “successful” like Elon Musk.
For 2 and 3, we imagine Elon Musk, Jeff Bezos, Bill Gates
For 4, “Forbes 30 under 30”, Balshree award in India.
For 5a, we imagine the journey of Mark Zuckerberg in the “Social Network”
For 5, We hear about these stories much more than 1 in 7billion times [5] because Mr. Zuckerburg is the worlds 2nd richest man
Are 1 to 5 expected to be connected? For example 2 is about bill gates and 5 is about mark Zuckerburg, do you expect a whole sentence to be about 1 person?
For 6, Elon musk is ranked 47 in billionares, Mark Zuckerburg is ranked 2 and Bill Gates is still #1. There are only 1000 people in the world who are worth more than 2 billion.
For 7, we think of a job as CEO of AMF.
For 8, Out of 7 billion people, it looks like there are about 1000 billionaire’s (worth >2 billion) as per forbes.
For 9, doing courses in Data Science
Claims
People like to Lionize [3]
My cousin who is 16 says he wants to be “successful” like Elon Musk [3]
[5a] is interesting[5] because they’re the exception[6]
We hear about Mark Zuckerburg much more than 1 in 7billion times [5] because he is the worlds 2nd richest man, and there are barely 1000 billionaire’s in the world[6].
I spent way too much time pondering about what example to give here, my confusion being how do you give an example to test “Something is interesting BECAUSE they are the exception”! I am aware that we can test, “Something is interesting AND it is also the exception”
If you want to get [7] then you’ll need [9]
Rob Mather from AMF became the founded and became the CEO of GiveWell’s top charity [7] by starting his career in sales and management [9]. He credited his skills to make AMF lean and efficient to his earlier work in sales and consulting.
P&E
(Most people)[1] reach the (peak of their impact)[2] in their (middle age)[3]. (Income)[4b] usually (peaks)[4c] in the 40s)[4], suggesting that it takes around 20 years for (most people)[5a] to reach their (peak productivity)[5]. Similarly, (experts)[6] only (reach their peak abilities)[7] between (age 30 to 60)[8], and if anything, (this age)[9a] is (increasing over time)[9].
For 1 & 5a, we think of Management Consultants(MC’s) who stay till they become partner at top firms, we think of Theoretical Physicists, Novel writers, Politicians (US President)
For 2 & 4b: It takes upto 20 years of working before reaching the scale of Senior Partner which makes bonuses in the order of millions (source). Donating 50% of that would be the peak of impact.
For 3 & 4: Graduation age of a Master is ~25, 20 years from there seems to be 40-45 (middle age)
For 5, we imagine becoming a senior partner at the top 3 firms
For 6, Scientists and economists
For 7, we think of people who win the Nobel Prize
For 8, Nobel prize winners have an average age of 47 (Source)
For 9, The average age of Nobel prize winners has increased by 6 years between the 20th and 21st century (source: TIO chapter 10).
For 9a: The average age of Nobel prize winners (47)
Claims
Most people reach [2] in middle age [3] ; 4b usually peaks in the 40s
Management consultants are able to earn (and hence donate) more than 600k$ with millions in bonuses starting from ages 40-45.
It takes 20 years for most people to reach their peak productivity
It takes 20 years after getting masters degree to become a senior partner
[6] reach their peak abilities at [8]
Scientists and Economists get Nobel prizes at average age of 47.
Age at which [6] reach their peak is increasing over time.
The average age for getting a Nobel Prize is increasing by 6 years when looking at a 100 year period starting in 1900’s.
P&E
When (researchers)[1] looked in (more detail)[2] at (these findings)[3], they found that (expert-level performance)[4] in (established)[5a] (fields)[5] requires (10-30 years)[6] of (focused practice)[7].
For 1, I imagine, K. Anders Ericsson and Martin Seligman
For 2, I imagine the “exploratory data analysis” I did for a course on the “energy usage over a 2-day period in February 2007”.
For 3, data that average Nobel Laureates age was 47.
For 4, ability to win the Olympic gold medal
For 5a, we look at the millions of videos on youtube on each aspect of figure skating like, two foot spin, crossovers etc…
For 5, Figure skating
For 6, we look at Shizuka Arakawa who started at the age of 5 and won the Olympic medal for Figure Skating at 24. Roughly 20 years later.
For 7, we imagine her persistence despite the ~20000 times she had derriere impacts on unforgiving ice while practicing her Ina Bauer.
Claims
[4] in [5a,5], requires 10-30 years of [7]
To get Olympic gold medal, in figure skating, Shizuka Arakawa spent 20 years from a young age of 5. She fell on her ass atleast 20000 times while practicing her specialty jump and managed to keep going.
P&E
K. Anders Ericsson, the (leader)[8a] of (this field of research)[8] who has been (working on it for over 30 years)[9], said: “I have (never found a convincing case)[10] for anyone (developing extraordinary abilities)[11] without (intense, extended practice)[12].”
For 8a: if we Google search “10000 hours skill practice”, on 3/4 hits of popular news outlets like BBC, you will find Anders Ericsson on it.
For 8: field answering how Shizuka Arakawa won the Olympic Medal
Is this not an example? What should it be then?
For 9, Anders has been publishing papers from 1990 until now (2019) on the topic related to “expertise in skills” (40 years).
For 11, Jerry Rice is one of the “greatest receivers” in NFL history. He has played 22 seasons and every game in every season except in 1997. No one has done this ever at the “receiver position”.
For 12, “His off season training’s were done 6 days a week. His workouts were known as the most demanding in the league, which other players would get sick before the end of the day. His trainer wouldn’t reveal the workouts because the trainer was afraid that people could injure themselves trying to duplicate it.” Source: TIO.
For 10, In the 1985 draft, fifteen teams passed him over before the San Francisco 49ers finally signed him, indicating that he was never going to be a legend. But he did become a legend, seemingly because of [12]
Claims
Never found a convincing case for [11] without [12]
In the 1985 draft, fifteen teams passed him over before the San Francisco 49ers finally signed him, indicating that he was never going to be a legend. But he did become a legend[11], seemingly because of [12].
P&E
(Mozart and Zuckerburg)[1] (succeeded)[2] while (young)[3] (because they started young)[4]. Mozart’s father was a (famous music teacher)[6], and (trained him intensely)[7] as a (toddler)[8].
For 1, we come back to the example of Shizuka Arakawa
For 2, we think of Olympic gold medal
For 3, we think of when she won her Olympic gold medal at 24
For 4, we think of her starting at the age of 5.
For 6: Leopold Mozart wrote a book on violin instruction which remained “influential” for “decades”.
For 7: !!!
In this case do I need to give an example of Mozart “getting trained intensely”? It’s hard to find them
For 8: Age 5 is when Mozart started learning music.
Claims
People like [1] succeeded young because they started young.
Shizuka Arakawa, got her gold Olympic medal at 24 while she started training at 5.
Marie Curie won the Nobel prize at 36, and she seemed to have started university when she was 24.
How will you test the claim with an example that someone succeeded young because they started young? I try to give 2 examples one of a person who started young, and the other of a person who started later and got her success later.
Mozart’s Father trained Mozart “intensely”[7] as a toddler.
I don’t have an example
P&E
(All this)[1a] (may sound like a bit of a downer)[2]: being (successful)[3] (takes time)[4]. But consider the (flip side)[5]: you can (improve)[6].
For 1a, we think of Shizuka Arakawa’s long journey of 20 years before winning the gold medal
For 2, I imagine the feeling that even after 50 hrs of training over 15 weeks, I missed 10 continuous shots in the game. I was like ‘what is the point of training and spending so much time per week!’.
For 3, Getting an Olympic Gold medal
For 4: takes 20 years
For 5,
Does it need an example, if so what is it? how do you give an example here?
For 6, Guy improving from 36% to 42% in 4 weeks courtesy of shooting 100 shots a day.
I am finding it hard to find one running example and split it among 1 to 6, am I expected to do that? Is it a requirement? In the claims I understand that it would all need to be from the same example.
Claims
Being successful takes time
Shizuka Arakawa won gold medal after 20 years of training
You can improve
Guy improving from 36% to 42% in 4 weeks
P&E
Lots of people come to us saying “I’m not sure I have any (useful skills)[1] to (contribute)[2]”. And that’s (often)[2a] true. If you’ve (just graduated)[3], you’ve probably spent the last four years (studying)[4] (Moby Dick, quantum mechanics, and Descartes)[5], and your (future job)[6] is (unlikely to involve)[7] any of (those things)[8].
For 2, I think of work at GiveWell
For 1, I think of programming, statistics, critical thinking
All skills that a typical ignorant Dutch person cannot understand; pure labels? Can you please give an example?
Cant believe I am spending more than 15-20 mins trying to come up with an example for skills or an equally unacceptable answer like below
“Interpreting and critiquing statistical analysis : A basic understanding of causal inference is helpful (for example, understanding the typical limitations of experimental, quasi-experimental, and observational methods; being able to quickly read and understand a regression table).”
For 2a, I think of myself as not fit for GiveWell level of statistics yet (I don’t know what regression table is).
For 3, I imagine what happened after I graduated from the mechanical engineering master
For 5, I think of subjects like non-linear dynamics, compliant mechanisms that I completed.
For 4, I think of getting 80% in the subject exams
For 6, I work in Machine Design, building modules that clamp wafers
For 7 & 8, I don’t use any of the things I learnt in my entire masters except for 1 book and only 4/10 chapters of it; let alone these being useful for EA work.
Claims
[6] is probably not going to need [5]
Dynamics, compliant mechanisms are not going to be useful for work at GiveWell.
I am not sure if I need to give examples for “likely”, “probably”.
P&E
However, (Ericsson’s research)[9] suggests that (anyone)[10] (can improve)[11] at many (skills)[12] with (focused practice)[13].
For 9, we think of the study with the violinists[TOI chapter 4].
For 10, I think of this guy and look at how much he sucked in the beginning
For 11, I think of Guy improving from 36% to 42% in 4 weeks
For 12, I think playing the guitar, chess, basketball, programming, and “critical thinking” as evident from TIO
I have an SST that my examples for skills are crap, can you weigh in?
For 13, I think of Jerry Rice, who did workouts for his conditioning 6 times a week which no one else could finish even once.
Not an example? Should be more like made 400 shots a day?
Claims
Anyone can improve skills [13]
This guy totally sucks when he started and after 7k hours he’s phenomenal.
P&E
Sure, (talent)[14] is (important)[15] too – if you’re 7-foot-tall it’s going to be (a lot easier)[16] to (get good)[17] at basketball – but that doesn’t mean (short people)[18] can’t still (improve their game)[19].
For 14, we think of bodybuilding where not everybody has the genes to look like Arnold or Dwayne the rock Johnson.
For 15, Without the right genes there is no point getting into bodybuilding and aiming to look like Arnold.
For 16, In the place where I live people who want to even play in the basketball team have to be 6 foot of higher
For 17, joining the NBA
For 18, Spud Webb was 5ft 7 inches, the shortest player to participate and win the NBA Slam Dunk Contest.
For 19: Guy improving from 36% to 42% in 4 weeks
Claims
[14] is important
“Good genes” like that of Arnold or Dwayne would help in winning Mr. Olympia competition.
If you’re 7 foot tall, it’s going to be [16] to [17]
In the place where I live people who want to even play in the basketball team have to be 6 foot of higher.
short people can improve their game
Spud Webb was 5ft 7 inches, the shortest player to participate and win the NBA Slam Dunk Contest.
P&E
This means even if you don’t feel you (have much to contribute)[20] now, you can become (much more skilled)[21] in the (future)[22], and probably (keep improving)[23] for (decades)[24].
For 20, we think of not being able to play Joe Satriani’s song “tears in the rain”
For 21, We think of this guitarist how he went from nothing to strictly phenomenal in 7000 hrs [22]
For 23 & 24,
“Jamie Dimon was an amazingly accomplished financial services executive at age twenty-nine, but he was much better at fifty, as CEO of JPMorgan Chase[21,22]”- (TIO pg179)
What is this “much better” you ask? I couldn’t think of other examples, than from the TIO
Claims
You can [21] in the future
We think of this guitarist how he went from nothing to strictly phenomenal in 7000 hrs (future)
You can probably keep improving for decades
“Jamie Dimon was an amazingly accomplished financial services executive at age twenty-nine, but he was much better at fifty, as CEO of JPMorgan Chase”
Statistics
Day 1: Sunday, 2.5 hrs DP, 3 hrs reading and “understanding” STM feedback, 1 hr adding math functionality to site and figuring out writing macros.
Started at 9:36. 4.7 hrs for basketball in that day.
Total phrases: 10
Day 2: Monday, 3.8 hrs of DP, 2.5 hrs gym, 8 hr work day
Started at 19:22 hrs, No sleep during work.
Total phrases: 35
Day 3: Tuesday, 5.3 hrs of DP, 2.5 hrs gym, 8 hr work day
Started at 17:32 hrs, 20 mins sleep during work.
Total phrases: 70
Day 4: Wednesday, 4.1 hrs of DP, 2 hrs in the gym, 8 hr work day
Started at 19:07 hrs, 15 mins sleep during work
Total phrases: 110
Day 5: Thursday, 4.0 hrs of DP, 2.5 hrs at the gym, 8 hr work day
Started at 19:21 hrs, 15 mins of sleep during work
Total phrases: 140
Day 6: Friday, 6 hrs of DP, no gym, 6 hr work day
Started at 15:10, 40 mins of sleep after 1 hr of work
Total phrases: 200
Finally, seemed to take forever. Failed to submit by the NIGHT.
Day 7: Saturday, 4 hrs of painful editing
Started at 09:43,
Re-writing, statistics, spell check
Total hours: 35 hrs
Total DP hours: 25.5 hrs
re-writing: 4 hrs
Reading and understanding feedback: 2.5 hrs
Fixing math in site: 1 hr
Total words: 8498 excluding quotes